|
 |
| Teachers.Net Gazette Vol.5 No.5 | May 2008 |
Subscribe for free home delivery |
|
Use Math's Magic to Intrigue Students Solving Linear Equations Once a math teacher gave the following problem in algebra to his students: Expand (a+b) n . | ||||||||||||||||||||||
| by Panamalai R. Guruprasad Regular contributor to the Gazette May 1, 2008 |
||||||||||||||||||||||
|
One student’s answer was as shown below:
The standard of math teaching in our schools, especially in countries like India, is not generally very good due to several reasons. Even in `sought after’ urban schools in cities like Chennai, where I come from, most students work hard to secure “rank” in board exams by memorizing than by understanding math concepts. Even those students who do understand math concepts do so because of facilities provided in their homes than due to classroom interactions. One main reason for this grim state of affairs is the lack of quality-oriented teacher development programs in colleges of education. Any serious observation into math and science teacher training programs can give an idea of what I mean by the above statement. Although there has always been some education commission or the other to suggest changes, their suggestions end up as stationary in office cupboards, one reason being that they are near idealistic or practically not possible to implement in our Indian scenario!
Like many of my colleagues, I have come across very difficult situations when teaching important concepts across the curriculum. My Bachelor of Education degree program, from one of the most reputed Universities, didn’t teach me how to cope with situations like these. [The status quo of our Education degree programs hasn’t changed much in the past 30 years, since I graduated]. However, I was not discouraged by the disadvantage. As the saying “Necessity is the mother of invention” goes, I could convert professional difficulties into opportunities. In fact, I learnt how to be a better teacher well after entering the profession In this article, I attempt to illustrate how I was able to teach how to solve “Linear equations” of the form y = ax + b, an important concept in middle school algebra, in my class in Bhutan, in 1978. Let me take an example “y = 3x + 5”. Our textbooks don’t generally go beyond the following steps in handling the equation:
Then they go to graphical representation by assigning values for x and y. From the nature of the graph (which will be a straight line) they get into defining the slope (=3) and the intercept (=5). As usual, I liked to deviate from the textbook treatment of the concept. I had to face the difficult situation in a school that was situated more than 3000 km from my hometown. I was partly homesick and partly uncertain as to whether I could survive in the remote village (which I reached a few days earlier, by traveling on a mud road for more than half a day). Within a few minutes of my having joined duty at the school, my headmaster handed me my teaching workload that included teaching linear equation to a class of 28 “eagerly awaiting” students. I was literally nervous as to how I was going to handle the situation. As usual, that evening, I tried to imagine my next day’s class; after analyzing different teaching strategies, I decided to use a play way method. The next morning, I entered the class, introduced myself as the new teacher who always saw mathematics as “magic” and “interesting” to live with. I also told my students that the magical element in mathematics helped me get many friends ever since I started learning the subject. As I was saying this, I could see my students excited. This was a great relief! Soon after the ice breaking session, I was able to introduce linear equation by announcing, “Children, we are going to do some magic, which all of you will enjoy. At the end of the period, you will know how to solve problems using linear equations. Perhaps you are wondering, how. Let me get to the point directly. We are dividing the class into two parts: you and me. You imagine any number in between 1 and 10. Multiply it by 3. Add 5. Tell me the number you get that way. I’ll tell you the number that you imagined. You can choose any 10 of your classmates with one number each. Go ahead.” Soon ten students came with their numbers, one after the other, and I could tell the number that they had imagined, without any problem. They were astonished. They could not control their curiosity of “How” (a crucially important motivator in mathematics) and requested me to disclose the “secret’. Now it was easy for me to disclose the secret: “For example: you imagined number 2. When you multiplied this number by 3, you got 6. When you added 5, it became 11 and hence you said that the resulting number was 11. I solved the puzzle by using the number you mentioned to me, by doing just the reverse of what you did, as shown below: What you did was: 2 X 3 = 6. 6 + 5 = 11. (The number that you imagined was 2 and the number you let me know was 11). What I did was: 11 – 5 = 6. 6/3 = 2 Then, I wrote the above problem (“magic”) in the equation form 3x + 5 = y on the chalkboard and asked students to identify the two variables, x (the number they imagined) and y (the final product in the operation). Then it was easy for them, after considering each “magical” example, to understand how I could solve the equation. They could see that while they used their x, and performed the operation 3x + 5 = y, I solved for x by performing the operation (y-5)/3. In other words, I did the reverse of what they did. This was exactly the core of the concept. I gave an opportunity for students to try the magic with their parents, siblings and others in their homes, that evening after school. The next morning, they all came with a far better understanding of the concept, and thanked me for teaching them an interesting “magic”! “Instructional practice should be informed by high-quality research, when available, and by the best professional judgment and experience of accomplished classroom teachers. High-quality research does not support the contention that instruction should be either entirely “student centered” or “teacher directed.” Research indicates that some forms of particular instructional practices can have a positive impact under specified conditions”. - National Mathematics Advisory Panel. Foundations for Success: The Final Report of the National Mathematics Advisory Panel, U.S. Department of Education: Washington, DC, 2008. p.14 cf. | ||||||||||||||||||||||
|


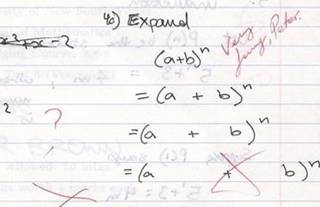
 Panamalai R Guruprasad works as Technical Advisor at the Inspectorate of Education attached to the Ministry of Education, Youth and Sports, Phnom Penh, Cambodia. His key professional responsibilities include developing and monitoring K-Grade 6 School Self Assessment Programs at the Central level.
He has served as teacher, principal and Education Officer in school systems in India, South Asia and Africa. He has also worked in Macmillan India Limited (an associate company of Macmillan UK), and Chandamama India Limited (the oldest kids magazine in India).
Panamalai R Guruprasad works as Technical Advisor at the Inspectorate of Education attached to the Ministry of Education, Youth and Sports, Phnom Penh, Cambodia. His key professional responsibilities include developing and monitoring K-Grade 6 School Self Assessment Programs at the Central level.
He has served as teacher, principal and Education Officer in school systems in India, South Asia and Africa. He has also worked in Macmillan India Limited (an associate company of Macmillan UK), and Chandamama India Limited (the oldest kids magazine in India).