|
 |
| Teachers.Net Gazette Vol.5 No.4 | April 2008 |
Subscribe for free home delivery |
|
Amusing Abacus Addition and subtraction of numbers can be taught using a resource that is inexpensive, colorful, amusing, absolutely child friendly and easy to make. The article explains how this marvelously simple resource, a math ‘toy’, can be used in our classrooms. | |||
| by Panamalai R. Guruprasad Regular contributor to the Gazette April 1, 2008 |
|||
|
Children find math to be very difficult. Most often, the problem lies in teaching learning processes taking place in our classrooms, particularly in third world countries. In countries like India, almost entire lesson materials come from textbooks that treat even fundamental concepts in a very superficial manner [a painful reality that I observed very closely, during my tenure in educational publishing]. I have come across numerous instances where textbooks have fallen short of pedagogic objectives. Teachers who use such materials not only confuse children but also make them dislike the subject. Let me take you down my memory lane, to the year 1998. The location is a K-5 elementary school in a large town in Southern India. One morning, a math teacher gives some homework to his children. That evening, children play math with broomsticks and empty matchboxes in their homes. But the parents are disappointed to see their wards playing instead of studying math. Next morning, they complain to the school principal about the teacher. The principal sends them back, assuring them that nothing has gone wrong and asks them to meet him after a week if they came across any problem. Meanwhile, the teacher likes to get out of the embarrassing situation and revert to ‘chalk and talk'. The principal asks him not to give up his experiment and assures him that he is on the right track. After a week, the same parents come back to tell that their kids love doing math with an unabated passion never seen anytime before! As the school principal, I am greatly relieved to see that my effort in training my colleague to make use of the ever-amusing abacus, has worked! Many of our math textbooks, particularly in countries like India, where I come from, introduce Abacus mainly to teach place value. Then they get to ‘Algorithms’, ‘Number line’or ‘Grouping’to introduce addition and subtraction of numbers. As teachers do not use much material beyond the textbook (due to time constraints), children are not given adequate exposure to follow algorithmic method without a clear understanding of how place value is applied in addition and subtraction operations. The most severe problem arises when teachers give abstract number problems (such as “21+13=?” instead of “There are 21 birds sitting on a tree. 13 more are joining them and they all leave for a weekend outing. How many birds are there in total?).
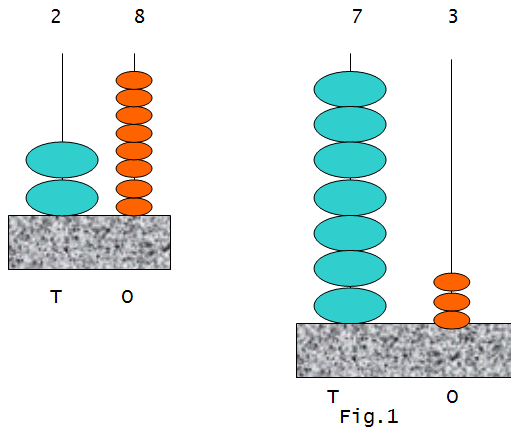
Two digit addition E.g. 28+73=? After explaining the Ones and Tens columns, by using a large model of the abacus, we can display the numbers 28 and 73 as shown in fig.1. I use different sized beads to let children understand the difference between the two place values (‘Tens’column represented as T and ‘Ones’column represented as O in the fig.) in a concrete manner.
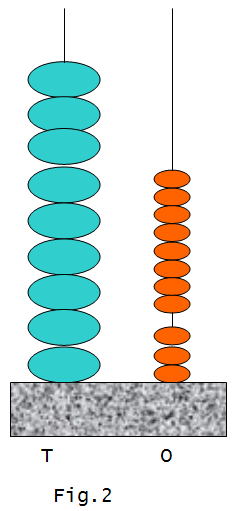
Next, we can add O beads and T beads and show a single resultant abacus as shown in fig.2.
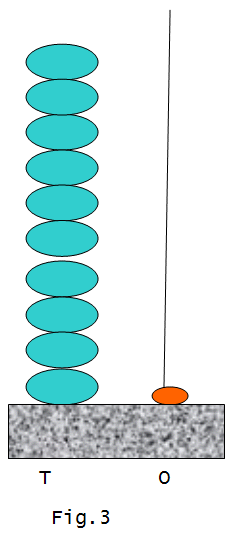
As there are 11 beads in the ‘Ones’column, 10 out of these (viz. 10 ‘O’s) can be converted as 1 ‘Ten’by replacing 10 ‘O’column beads by 1 ‘Ten’s column bead. The resultant will look like in fig.3.
Now it is easy for children to count the beads in the ‘Ones’and ‘Tens’column. They will see that it is 10 ‘Tens’and 1 ‘One’. That is, 101. The algorithmic equivalent (showing the carrying over of number 1) in 28 + 73 is as follows:
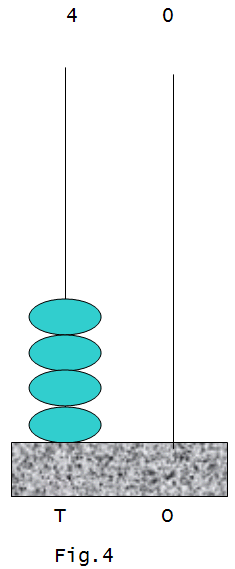
If we teach 28 + 73 by using algorithm before using abacus, children are mostly likely to encounter problems in understanding the carry over concept. Two digit subtraction Likewise, the concept of ‘borrowing’in subtraction can only be understood if we use abacus in performing the actual number operation as the following illustrations show. Eg.40–23=? The number 40 is represented in the abacus as shown in fig.4.
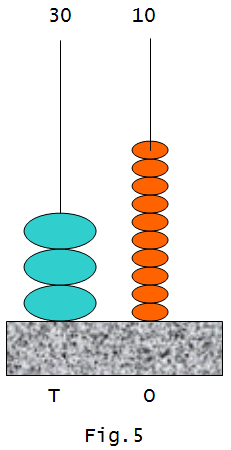
Our problem is to remove 23 out of 40. We can demonstrate the concept by replacing 1 bead from the ‘Tens’column [one large bead] by 10 ‘One’s in the abacus. Then, the abacus will look as in fig.5.
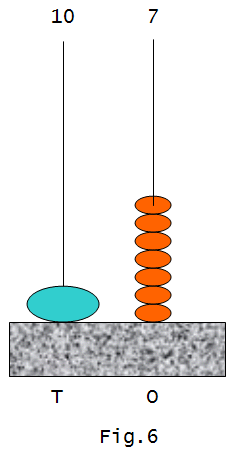
Now, we can remove 2 ‘tens’[two large beads] and 3 ‘ones’[3 small beads] and arrive at the result [40 – 23 = 17] as shown in fig.6.
I have enjoyed working with children as they come up with their own elegantly looking fully functional abacuses (which they call “math toy”) that they made using color beads, drinking straws, cardboard cartons and such other items that are usually discarded in our homes after use. | |||
|


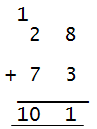
 Panamalai R Guruprasad works as Technical Advisor at the Inspectorate of Education attached to the Ministry of Education, Youth and Sports, Phnom Penh, Cambodia. His key professional responsibilities include developing and monitoring K-Grade 6 School Self Assessment Programs at the Central level.
He has served as teacher, principal and Education Officer in school systems in India, South Asia and Africa. He has also worked in Macmillan India Limited (an associate company of Macmillan UK), and Chandamama India Limited (the oldest kids magazine in India).
Panamalai R Guruprasad works as Technical Advisor at the Inspectorate of Education attached to the Ministry of Education, Youth and Sports, Phnom Penh, Cambodia. His key professional responsibilities include developing and monitoring K-Grade 6 School Self Assessment Programs at the Central level.
He has served as teacher, principal and Education Officer in school systems in India, South Asia and Africa. He has also worked in Macmillan India Limited (an associate company of Macmillan UK), and Chandamama India Limited (the oldest kids magazine in India).